Hier werden vor allem Geräte vorgestellt, bei denen Rechen-Aufgaben gestellt werden und - von Schülern und Schülerinnen - gelöst werden sollen, meist mit Ergebniskontroll-Einrichtung. 

Andere Lernhilfen sind bspw. Bruch- und Fingerrechenapparate.

[Seite noch im Aufbau ...]

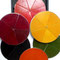
Bruchrechenapparat aus Frankreich - Set bestehend aus 4 Äpfeln mit einem ganzen, einem halbierten, einem gedrittelten und einem geviertelten Apfel.

Aus Frankreich; ein Apfel mit Stempel Déposé (= Pat. angem.).

12,6x12,6x5 cm; 307 gr. (jeweils kompl. Box); Æ Apfel 5,8 cm

Sehr ähnlich, aber deutlich einfacher konstruiert als der Bruchrechenapparat Archimedes: dieses Set besteht aus 9 Äpfeln, bei denen sich die einzelnen Segmente von der Mittelachse herausklappen lassen. Siehe dessen Patent DE489439 aus 1927.

Es gab auch den Bruchrechner Astronom von Heinrich Pflaum aus Weilderstadt (ca. 1929), ein Set aus 4 Äpfeln, ähnlich wie vor, aber unterschiedliche Segmente (s.u.).

Bruchrechenapparat Kleinsorge(?) Vollbrecht (Namensstempel - auch auf einem anderen Expl. - kaum lesbar, insb. die Vokale nicht)

x cm; x gr.

Holzbox mit 10 Blechtellern mit je 1 bis 10 Holzteilen, die jeweils eine volle Scheibe bilden bzw. Brüche von 1/10 bis 1/1 abbilden.

Ich konnte nichts dazu ergoogeln, deshalb keine Altersangabe. Wer weiß was?

hergestellt von Heinrich Pflaum aus Weilderstadt

DRGM 1069720 aus 1929

12,6x12,6x6,7 cm; 443 gr. (jeweils kompl. Box); Æ Apfel 5,6cm, h 6,3 cm

In der 8-Seitigen Anleitung nimmt Hrch. Pflaum Bezug auf Kepler und die Psychologie: um einen Begriff (hier Bruchrechnen) vollkommen und schnell zu erfassen, sei es nötig, dass man begrifflich denken lernt (hier mithilfe der Rechenäpfel). "Strahlen der Erkenntnis hat die Anschauung dieses figürlich 'Überzeugen' ausgelöst", so ein Lehrer.

Die vier Äpfel des Sets haben je 4-7 teils unterschiedliche Segmente, die sich per Drehknopf lösen/arretieren lassen und ausklappbar sind.

Apfel 1: 1/2 + 1/4 + 2/8

Apfel 2: 1/3 + 2/6 + 3/9

Apfel 3: 4/5 + 2/10

Apfel 4: 7/7

Weilderstadt ist der Geburtsort von Johannes Kepler, deshalb wohl der Name ASTRONOM.

Link: Anleitung (diese zeigt auch das Geburtshaus Keplers und das Herstellerhaus von Hrch. Pflaum)

hergestellt von The Educational Device Co., Medina, N.Y., USA

Ø 20,5 cm; Höhe 1,2 cm; 318 g; um 1930; mit aufgedruckter Anleitung

"a delightful game for speedily learning the facts of arithmetic"

Das eine meiner beiden Expl. stellt auf beiden Scheiben Aufgaben zur Division (erste 5 Photos) und zeigt dann nach Drehen der Scheibe mit dem Metallhaken an, ob man die richtige Lösung errechnet hat. Das zweite Expl. ist mit Addition beschriftet und ansonsten außen identisch (letze 4 Photos), enthält aber eine Scheibe mit Aufgaben zur Addition und eine zur Subtraktion.

Es gibt auch Expl. für Multiplikation, Brüche und Kolonnenaddition (s.u.).

hergestellt von The Educational Device Co., Medina, N.Y., USA

x cm; x g; um 1930

Im Holzkasten mit jeweils einer Rechenscheibe im Boden und Deckel, mit aufgeklebter Anleitung unter dem Boden. Wirkt älter als die Metallvariante(?).

"Drill tests now ready - all thorough scientific drills."

Die beiden identischen Scheiben stellen Aufgaben zur Kolonnenaddition und zeigen dann nach Drehen der Scheibe mit dem Metallhaken an, ob man die richtige Lösung errechnet hat.

herausgegeben von Edizioni Badalamenti, Bergamo, Italien

(entwickelt von Gaetano Roberto Badalamenti)

hergestellt (Schieber) von Litoplast, Cinisello, Mailand, Italien

16x5,4x0,2 cm (Rechner); 12 gr. (ohne Etui) 

produziert um 1960; Patent z.B. AT211582 "Rechenschieber zur Ermittlung der Teilbarkeit und Teilung in Faktoren von Zahlen" von 1958/60.

In rotem Plastiketui mit Anleitung; Etui beschrieben in engl.,  frz., dt.+ital.

In der Anleitung wird der Rechner Regolo Badalamenti bezeichnet.

Man kann für Zahlen bis 3199 ablesen, durch welche Zahlen diese teilbar sind (Zerlegung in Primzahlen). Für 645 ergibt sich bspw. teilbar durch 3, 5 und 43; für 1567, dass Primzahl. Etwas knifflig beim Einstellen und Ablesen.

Den gleichen Rechner gibt es auch heute noch als SCOMPOSIT in gleicher Größe sowie zum Vorführen in der Schulklasse in der Größe 98x33 cm.

Link: Erläuterungen zum Regolo della Divisibilita 

entwickelt von Egerton Smith (1774-1841) und William Dolier (1790er-1869) aus Liverpool

produziert bzw. beworben/beschrieben mind. von 1830-1842

verkauft von J. Phelps, London; Thomas Taylor, Liverpool; Wrightson and Webb, Birmingham; and all Booksellers; Preis: 2₤ 2S pro Set

Set bestehend aus 4 Holz-Boxen je 31,8x12,3x2,2 cm; je rund 500 gr.

Designed for the use of schools (Gruppenarbeit bis 4 Schüler) and private families.

a) Arithmetical Scales for simple addition (Abb. 1-3): Let the Pupil add them up, placing the answer on his slate.

b) Arithmetical Scales for simple subtraction (Abb. 4-6): Let the Pupil subtract the lower line from the upper, placing the answer on his slate.

c) Arithmetical Scales for simple multiplication (Abb. 7-9): It will be seen that this sum is to be multiplied by 2, in doing which set down the product on the slate; and the proof will be found ....

d) Arithmetical Scales for simple division (Abb. 10-12): It is evident that this sum is to be divided by 2, in doing which set down the product on the slate; and the proof will be found...

Durch Drehen der Stäbe werden verschiedene Aufgaben gestellt, die man auf seiner Tafel ausrechnen soll. Zum Abgleich kann das korrekte Ergebnis dann auf einem anderen Stab abgelesen werden.

Komplettes Set, sehr schön erhalten, obschon bald 200 Jahre alt.

Von Smith und Dolier gab es bspw. auch Smith & Dolier's copy-books, delible ink, white tablet, playful teacher und Smith's "key to reading".

hergestellt von Lehrer W. Wlecke, Gütersloh

vertrieben von seinem Grundschulverlag in Gütersloh i.W.

produziert von 1919 (Patent DE331979 erteilt zum 05.03.1919) bis ca. 1930

2x10 Finger (rot und weiß); 44x14,5x24 cm; 2,7 kg

Dieses Lehr- und Lernmittel unterscheidet sich bzgl. Optik und Methodik deutlich von anderen Lehrmitteln, die meist auf Kugelrechnern basierten. Für Lehrer Wlecke war dies die einzige sinnvolle Methode, rechenschwachen Kindern die Grundlagen der Arithmetik beizubringen (Anthes). Anleitung siehe u.g. Buch von Wlecke.

In einem Holzkoffer sind 2 Hände mit je 5 roten und 5 weißen Klapp-Fingern angebracht, insgesamt also 20 Klappfinger. Im Boden befindet sich eine Klappe mit Kurzanleitung.

Highlight in jeder Sammlung und Ausstellung.

Dazu noch das in Wleckes Buch beschriebene Zubehör

- Finger-Rechen-Hunderter-Tafeln mit roten Winkelpappen und grün-transparenten Abdeckwinkeln (kleine Ausführung für den Schüler) - Abb. 6+7 - Im Buch auf S. 29-38 und 63 beschrieben.

- Finger-Rechen-Einmaleins für den Schüler zum Einzeichnen von 2 Farben - Abb. 7+8 - Im Buch auf S. 54f und 64-66 beschrieben.

Auf Seite 67 werden beide - zusammen mit den anderen Lehrmaterialien des "Grundschulverlag in Gütersloh" - aufgeführt; natürlich auch Wlecke's Finger-Rechen-Apparate (gr/kl) und -Spielzeug sowie "Kastrup's Lese- und Rechenmaschine".

Im Ruhestand hat W. Wlecke 1953 ein weiteres Gerät namens Kreis-Bruch-Rechen-Apparat als DBGM (Nr. 1686075) eintragen lassen.

Links+Literatur: "Die Finger als Fundament des ganzen Zahlenbaues" von W. Wlecke, 1929; "Gütersloher Patentrechner" in Carl, 2017; "Rechnen mit den Fingern", HNF, 05.2022